Machine Learning for Physics and Astronomy
Christoph Weniger
Monday, 10 May 2021
Chapter 3: Convolutional neural networks
\(\newcommand{\indep}{\perp\!\!\!\perp}\)
A little history
Visual perception (Hubel and Wiesel, 1959-1962)
- David Hubel and Torsten Wiesel discover the neural basis of visual perception.
- Awarded the Nobel Prize of Medicine in 1981 for their discovery.
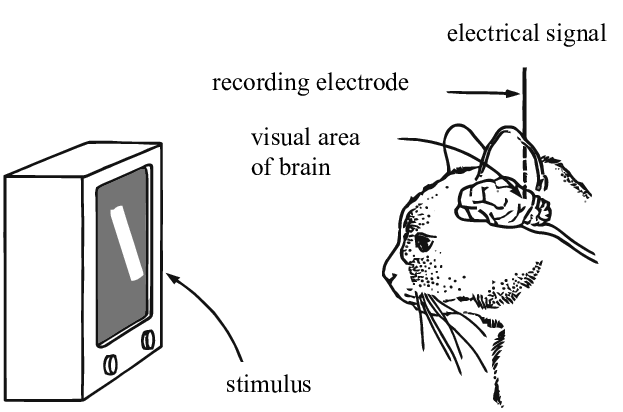


Hubel and Wiesel
Hubel and Wiesel
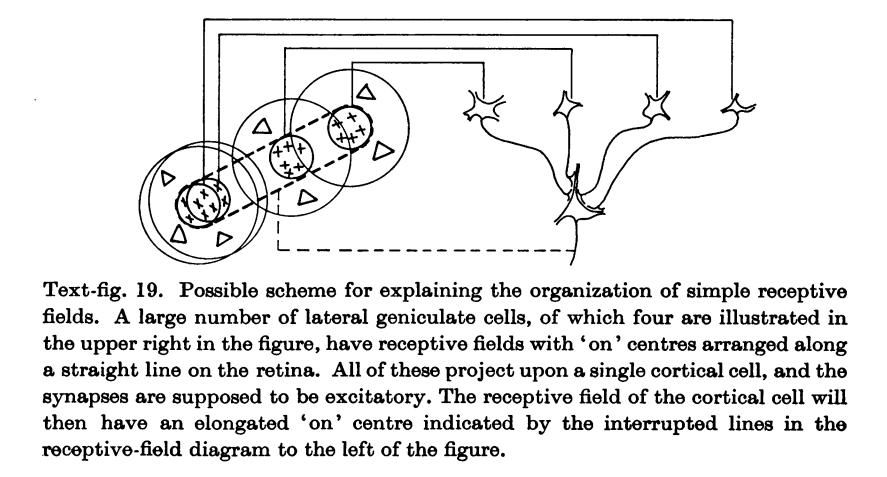
Credits: Hubel and Wiesel, Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex, 1962.
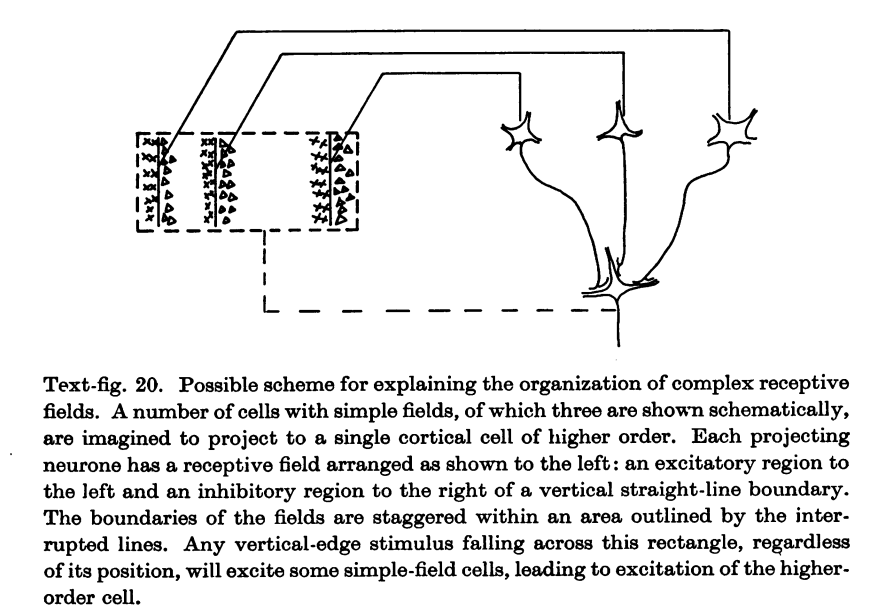
Credits: Hubel and Wiesel, Receptive fields, binocular interaction and functional architecture in the cat’s visual cortex, 1962.
Neocognitron (Fukushima, 1980)
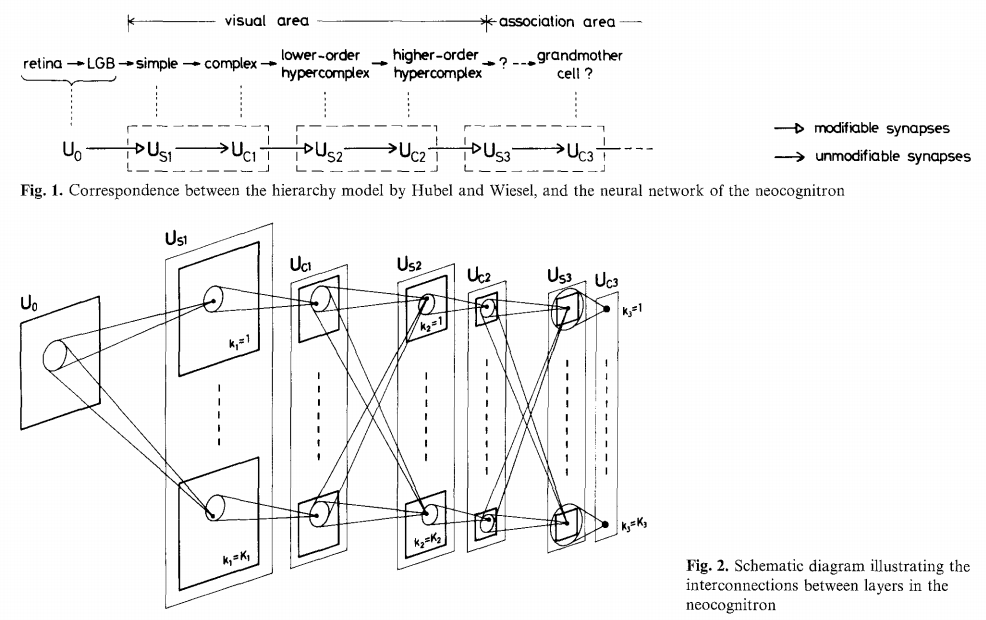
Fukushima proposes a direct neural network implementation of the hierarchy model of the visual nervous system of Hubel and Wiesel.
Credits: Kunihiko Fukushima, Neocognitron: A Self-organizing Neural Network Model, 1980.
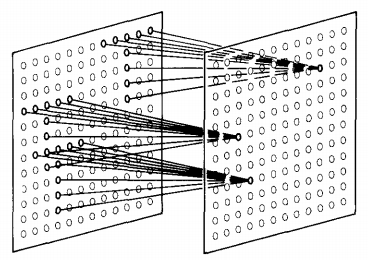
Convolutions
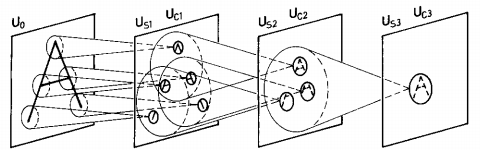
Feature hierarchy
Credits: Kunihiko Fukushima, Neocognitron: A Self-organizing Neural Network Model, 1980.
- Built upon convolutions and enables the composition of a feature hierarchy.
- Biologically-inspired training algorithm, which proves to be largely inefficient.
Backpropagation (Rumelhart et al, 1986)
- Rumelhart and Hinton introduce backpropagation in multi-layer networks with sigmoid non-linearities and sum of squares loss function.
- They advocate for batch gradient descent in supervised learning.
- Discuss online gradient descent, momentum and random initialization.
- Depart from biologically plausible training algorithms.

Credits: Rumelhart et al, Learning representations by back-propagating errors, 1986.
Convolutional networks (LeCun, 1990)
- LeCun trains a convolutional network by backpropagation.
- He advocates for end-to-end feature learning in image classification.

Credits: LeCun et al, Handwritten Digit Recognition with a Back-Propagation Network, 1990.
LeNet-1 (LeCun et al, 1993)
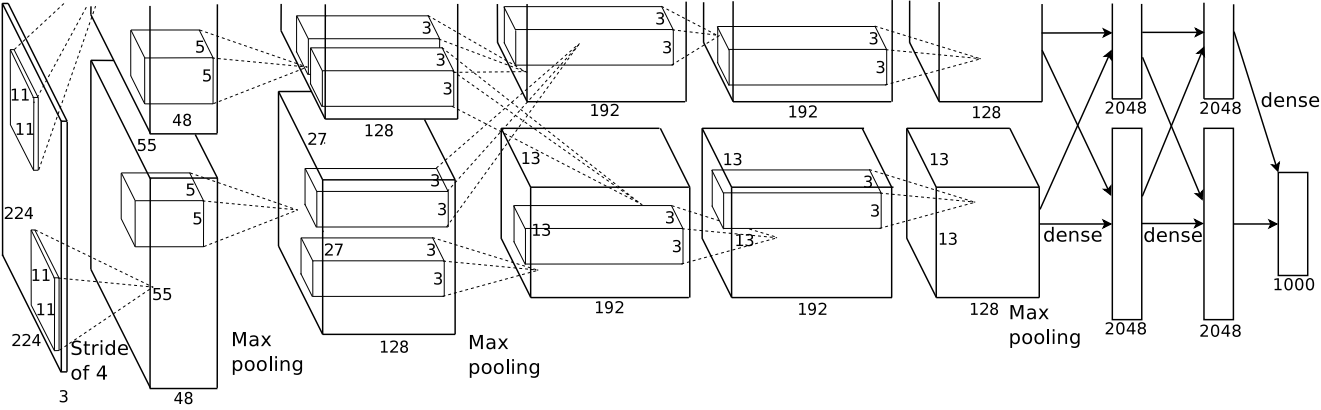
AlexNet (Krizhevsky et al, 2012)
- Krizhevsky trains a convolutional network on ImageNet with two GPUs.
- 16.4% top-5 error on ILSVRC’12, outperforming all other entries by 10% or more.
- This event triggers the deep learning revolution.
Convolutions
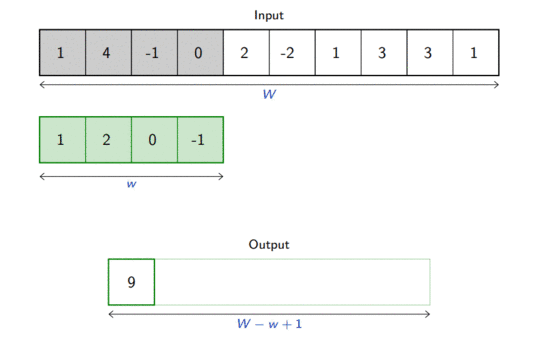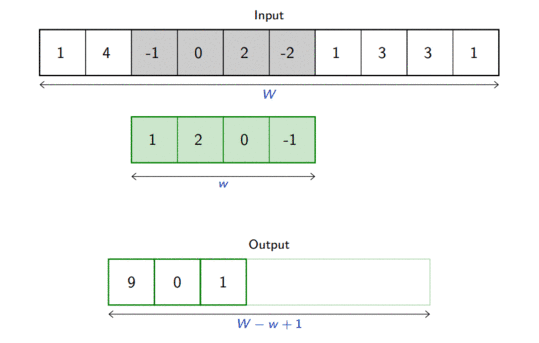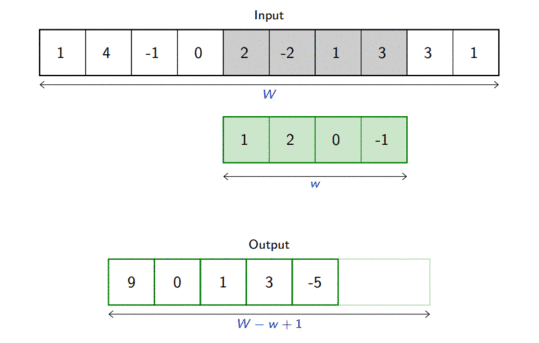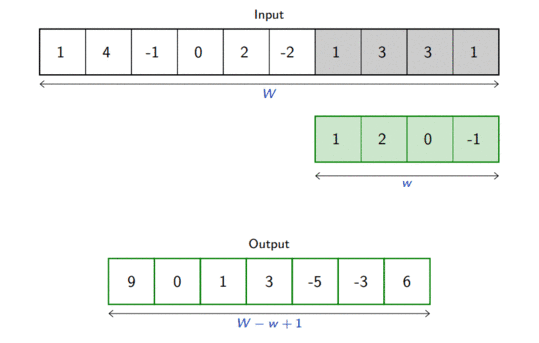
For one-dimensional tensors, given an input vector \(\mathbf{x} \in \mathbb{R}^W\) and a convolutional kernel \(\mathbf{u} \in \mathbb{R}^w\), the discrete convolution \(\mathbf{x} \circledast \mathbf{u}\) is a vector of size \(W - w + 1\) such that \[\begin{aligned} (\mathbf{x} \circledast \mathbf{u})[i] &= \sum_{m=0}^{w-1} x_{m+i} u_m . \end{aligned} \]
Note: Technically, \(\circledast\) denotes the cross-correlation operator. However, most machine learning libraries call it convolution.
Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
Convolutions can implement differential operators: \[(0,0,0,0,1,2,3,4,4,4,4) \circledast (-1,1) = (0,0,0,1,1,1,1,0,0,0) \]

or crude template matchers:

Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
Convolutions generalize to multi-dimensional tensors:
- In its most usual form, a convolution takes as input a 3D tensor \(\mathbf{x} \in \mathbb{R}^{C \times H \times W}\), called the input feature map.
- A kernel \(\mathbf{u} \in \mathbb{R}^{C \times h \times w}\) slides across the input feature map, along its height and width. The size \(h \times w\) is the size of the receptive field.
- At each location, the element-wise product between the kernel and the input elements it overlaps is computed and the results are summed up.
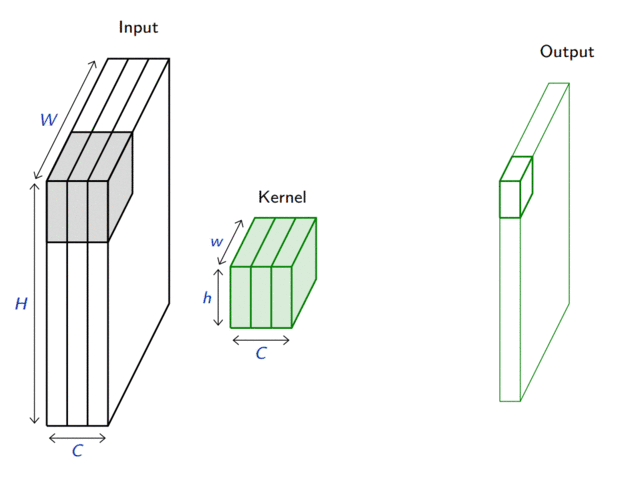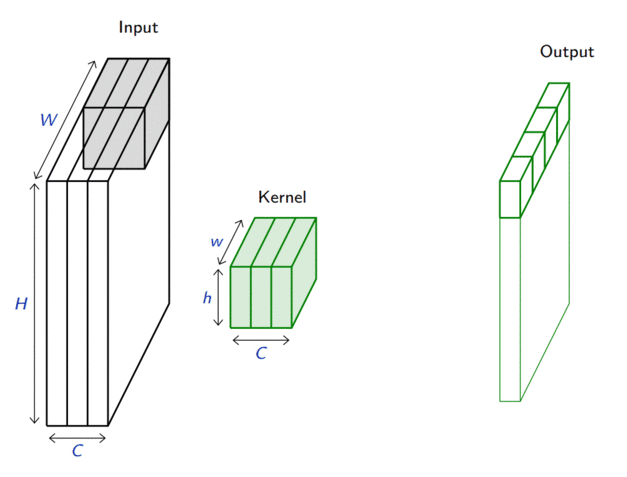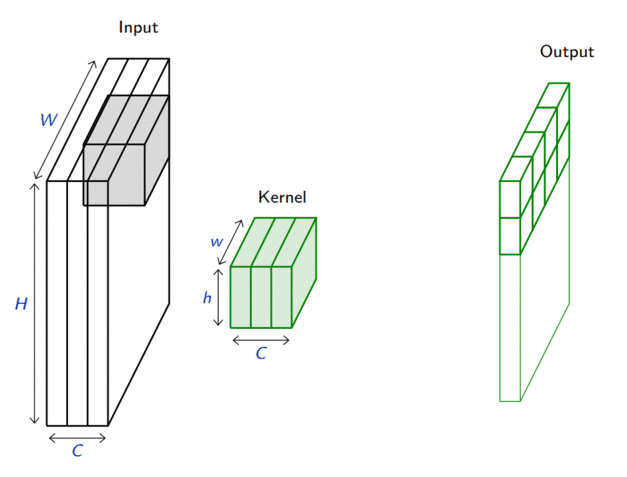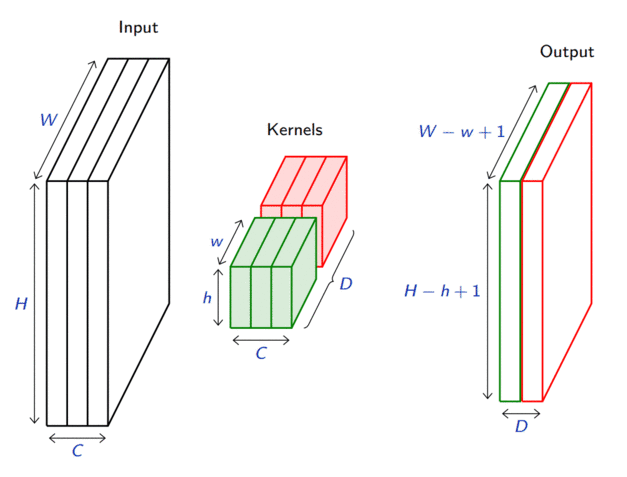
Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
- The final output \(\mathbf{o}\) is a 2D tensor of size \((H-h+1) \times (W-w+1)\) called the output feature map and such that: \[\begin{aligned} \mathbf{o}_{j,i} &= \mathbf{b}_{j,i} + \sum_{c=0}^{C-1} (\mathbf{x}_c \circledast \mathbf{u}_c)[j,i] = \mathbf{b}_{j,i} + \sum_{c=0}^{C-1} \sum_{n=0}^{h-1} \sum_{m=0}^{w-1} \mathbf{x}_{c,n+j,m+i} \mathbf{u}_{c,n,m} \end{aligned}\] where \(\mathbf{u}\) and \(\mathbf{b}\) are shared parameters to learn.
- \(D\) convolutions can be applied in the same way to produce a \(D \times (H-h+1) \times (W-w+1)\) feature map, where \(D\) is the depth.
- Swiping across channels with a 3D convolution usually makes no sense, unless the channel index has some metric mearning.
Convolutions have three additional parameters:
- The padding specifies the size of a zeroed frame added arount the input.
- The stride specifies a step size when moving the kernel across the signal.
- The dilation modulates the expansion of the filter without adding weights.
Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
Padding
Padding is useful to control the spatial dimension of the feature map, for example to keep it constant across layers.
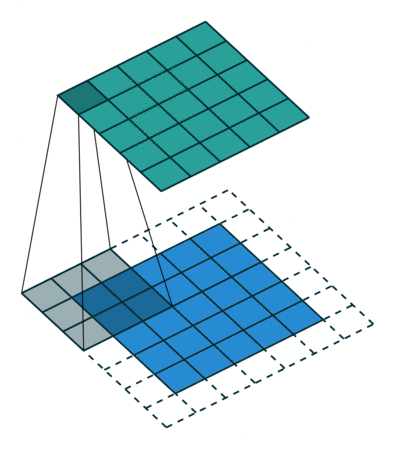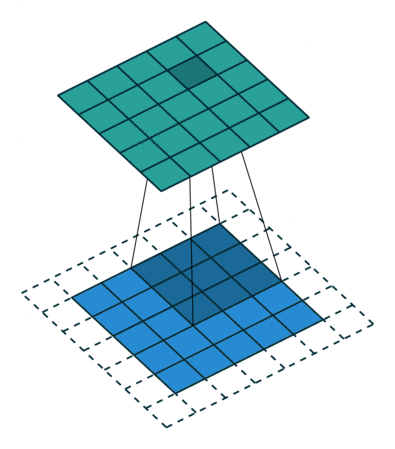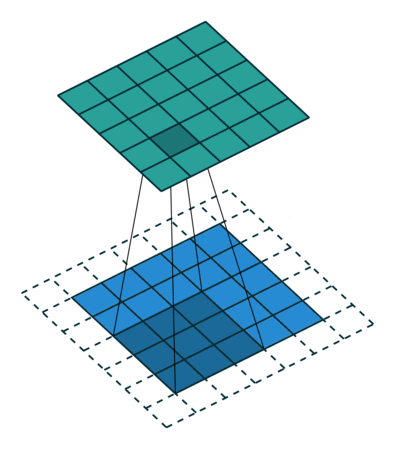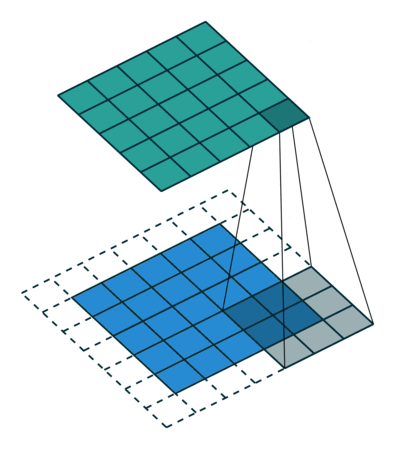
Credits: Dumoulin and Visin, A guide to convolution arithmetic for deep learning, 2016.
Strides
Stride is useful to reduce the spatial dimension of the feature map by a constant factor.
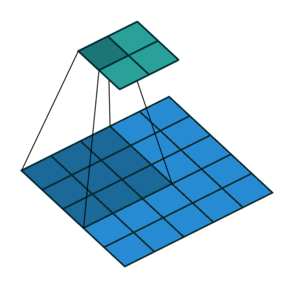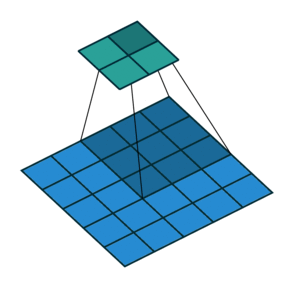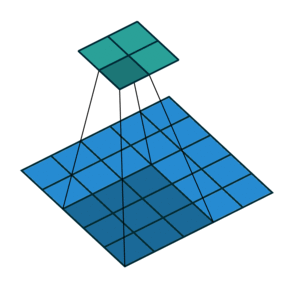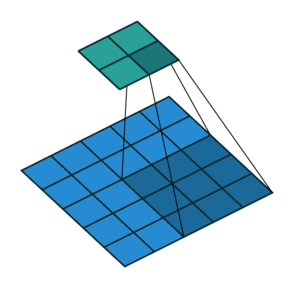
Credits: Dumoulin and Visin, A guide to convolution arithmetic for deep learning, 2016.
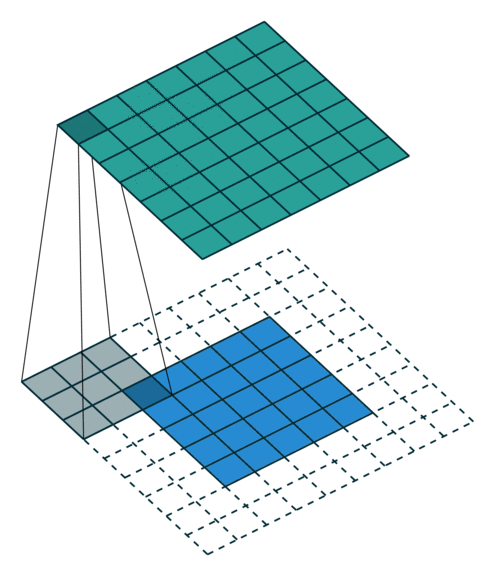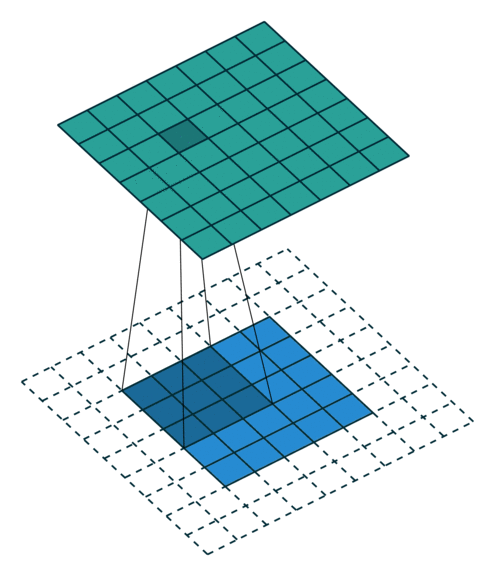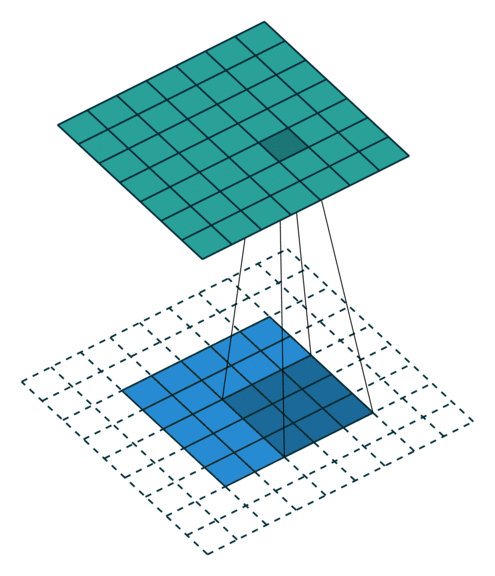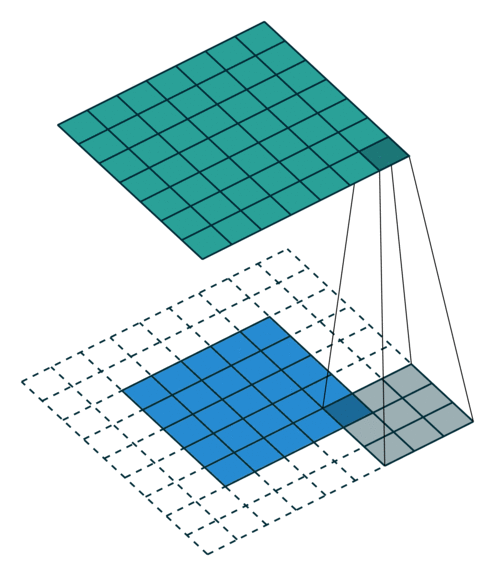
Dilation
The dilation modulates the expansion of the kernel support by adding rows and columns of zeros between coefficients.
Having a dilation coefficient greater than one increases the units receptive field size without increasing the number of parameters.
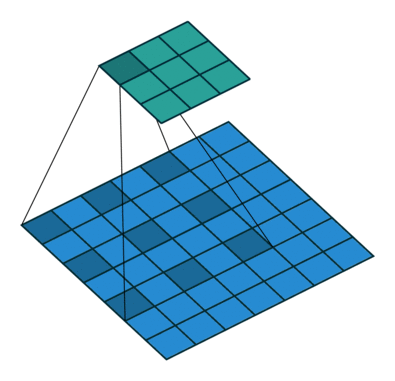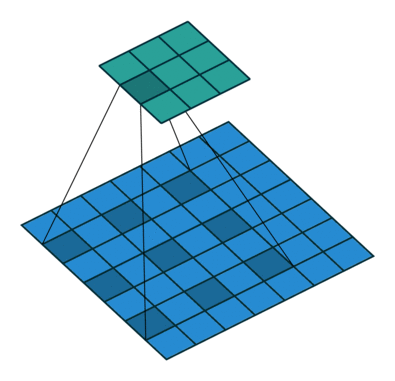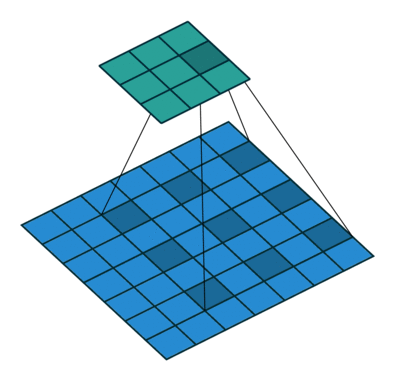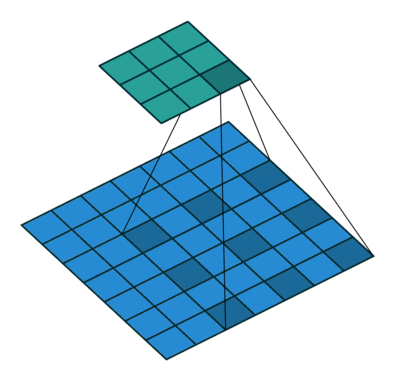
Credits: Dumoulin and Visin, A guide to convolution arithmetic for deep learning, 2016.
Equivariance
A function \(f\) is equivariant to \(g\) if \(f(g(\mathbf{x})) = g(f(\mathbf{x}))\).
- Parameter sharing used in a convolutional layer causes the layer to be equivariant to translation.
- That is, if \(g\) is any function that translates the input, the convolution function is equivariant to \(g\).

If an object moves in the input image, its representation will move the same amount in the output.
Credits: LeCun et al, Gradient-based learning applied to document recognition, 1998.
- Equivariance is useful when we know some local function is useful everywhere (e.g., edge detectors).
- Convolution is not equivariant to other operations such as change in scale or rotation.
Convolutions as matrix multiplications
As a guiding example, let us consider the convolution of single-channel tensors \(\mathbf{x} \in \mathbb{R}^{4 \times 4}\) and \(\mathbf{u} \in \mathbb{R}^{3 \times 3}\):
\[ \mathbf{x} \circledast \mathbf{u} = \begin{pmatrix} 4 & 5 & 8 & 7 \\ 1 & 8 & 8 & 8 \\ 3 & 6 & 6 & 4 \\ 6 & 5 & 7 & 8 \end{pmatrix} \circledast \begin{pmatrix} 1 & 4 & 1 \\ 1 & 4 & 3 \\ 3 & 3 & 1 \end{pmatrix} = \begin{pmatrix} 122 & 148 \\ 126 & 134 \end{pmatrix}\]
The convolution operation can be equivalently re-expressed as a single matrix multiplication:
- the convolutional kernel \(\mathbf{u}\) is rearranged as a sparse Toeplitz circulant matrix, called the convolution matrix: \[\mathbf{U} = \begin{pmatrix} 1 & 4 & 1 & 0 & 1 & 4 & 3 & 0 & 3 & 3 & 1 & 0 & 0 & 0 & 0 & 0 \\ 0 & 1 & 4 & 1 & 0 & 1 & 4 & 3 & 0 & 3 & 3 & 1 & 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 0 & 1 & 4 & 1 & 0 & 1 & 4 & 3 & 0 & 3 & 3 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 1 & 4 & 1 & 0 & 1 & 4 & 3 & 0 & 3 & 3 & 1 \end{pmatrix}\]
- the input \(\mathbf{x}\) is flattened row by row, from top to bottom: \[v(\mathbf{x}) = \begin{pmatrix} 4 & 5 & 8 & 7 & 1 & 8 & 8 & 8 & 3 & 6 & 6 & 4 & 6 & 5 & 7 & 8 \end{pmatrix}^T\]
Then, \[\mathbf{U}v(\mathbf{x}) = \begin{pmatrix} 122 & 148 & 126 & 134 \end{pmatrix}^T\] which we can reshape to a \(2 \times 2\) matrix to obtain \(\mathbf{x} \circledast \mathbf{u}\).
A convolutional layer is a special case of a fully connected layer.
Convolution view
Fully connected view
Pooling
When the input volume is large, pooling layers can be used to reduce the input dimension while preserving its global structure, in a way similar to a down-scaling operation.
Pooling
Consider a pooling area of size \(h \times w\) and a 3D input tensor \(\mathbf{x} \in \mathbb{R}^{C\times(rh)\times(sw)}\).
- Max-pooling produces a tensor \(\mathbf{o} \in \mathbb{R}^{C \times r \times s}\) such that \[\mathbf{o}_{c,j,i} = \max_{n < h, m < w} \mathbf{x}_{c,rj+n,si+m}.\]
- Average pooling produces a tensor \(\mathbf{o} \in \mathbb{R}^{C \times r \times s}\) such that \[\mathbf{o}_{c,j,i} = \frac{1}{hw} \sum_{n=0}^{h-1} \sum_{m=0}^{w-1} \mathbf{x}_{c,rj+n,si+m}.\]
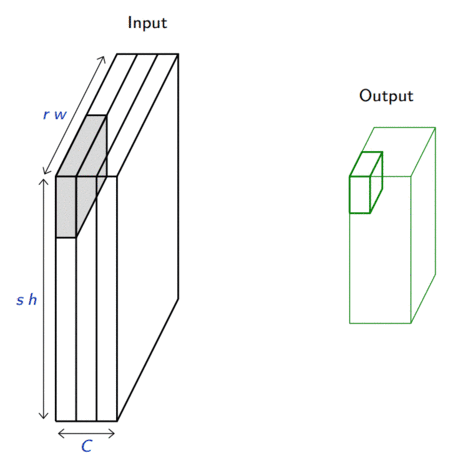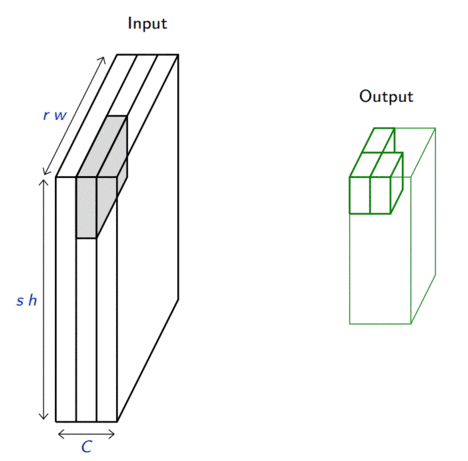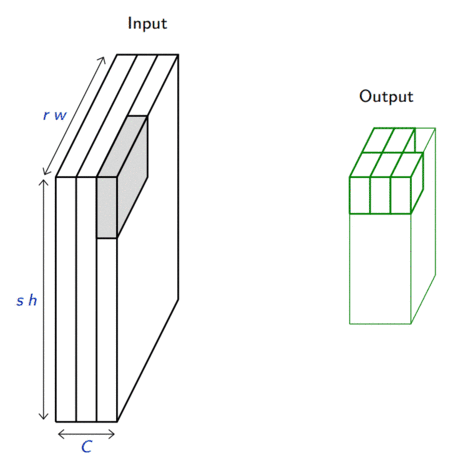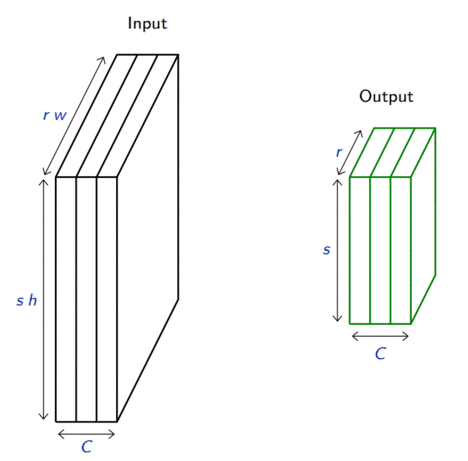
Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
Invariance of Pooling layers
- Pooling layers provide invariance to any permutation inside one cell.
- It results in (pseudo-)invariance to local translations.
- This helpful if we care more about the presence of a pattern rather than its exact position.
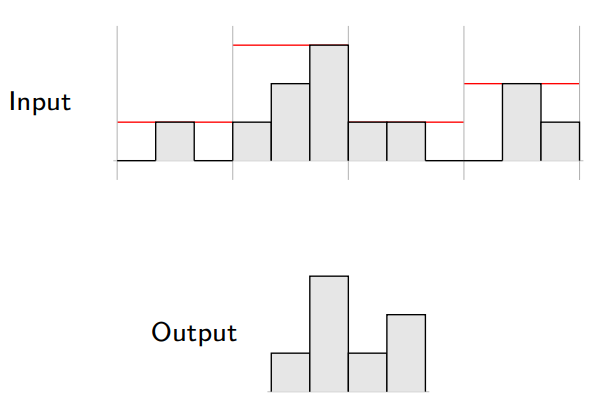
Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
Convolutional networks
A convolutional network is generically defined as a composition of convolutional layers (\(\texttt{CONV}\)), pooling layers (\(\texttt{POOL}\)), linear rectifiers (\(\texttt{RELU}\)) and fully connected layers (\(\texttt{FC}\)).
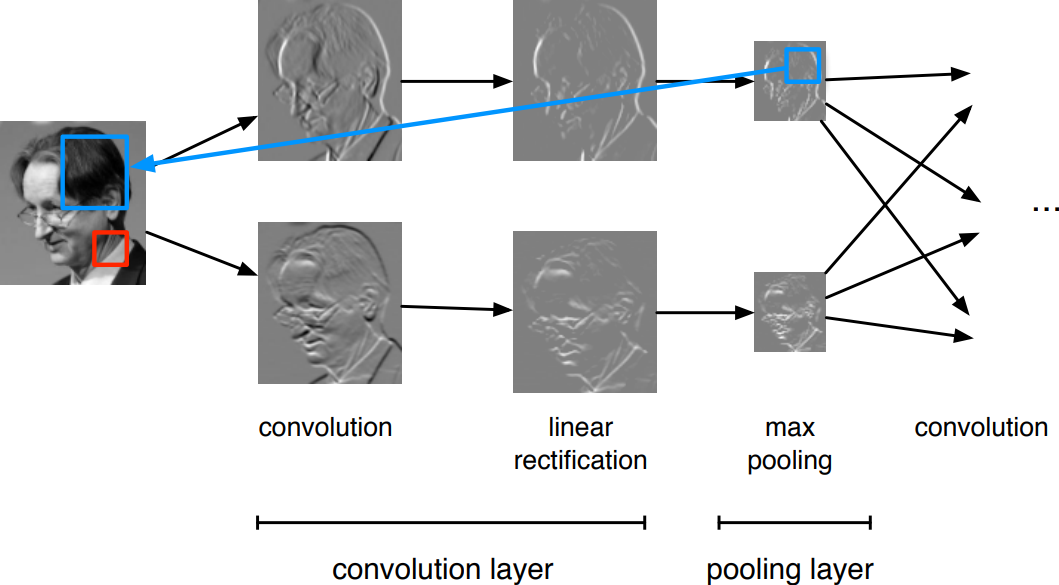
The most common convolutional network architecture follows the pattern:
\[\texttt{INPUT} \to [[\texttt{CONV} \to \texttt{RELU}]\texttt{*}N \to \texttt{POOL?}]\texttt{*}M \to [\texttt{FC} \to \texttt{RELU}]\texttt{*}K \to \texttt{FC}\]
where:
- \(\texttt{*}\) indicates repetition;
- \(\texttt{POOL?}\) indicates an optional pooling layer;
- \(N \geq 0\) (and usually \(N \leq 3\)), \(M \geq 0\), \(K \geq 0\) (and usually \(K \leq 2\));
- the last fully connected layer holds the output (e.g., the class scores).
Some common architectures for convolutional networks following this pattern include:
- \(\texttt{INPUT} \to \texttt{FC}\), which implements a linear classifier (\(N=M=K=0\)).
- \(\texttt{INPUT} \to [\texttt{FC} \to \texttt{RELU}]{*K} \to \texttt{FC}\), which implements a \(K\)-layer MLP.
- \(\texttt{INPUT} \to \texttt{CONV} \to \texttt{RELU} \to \texttt{FC}\).
- \(\texttt{INPUT} \to [\texttt{CONV} \to \texttt{RELU} \to \texttt{POOL}]\texttt{*2} \to \texttt{FC} \to \texttt{RELU} \to \texttt{FC}\).
- \(\texttt{INPUT} \to [[\texttt{CONV} \to \texttt{RELU}]\texttt{*2} \to \texttt{POOL}]\texttt{*3} \to [\texttt{FC} \to \texttt{RELU}]\texttt{*2} \to \texttt{FC}\).
Note that for the last architecture, two \(\texttt{CONV}\) layers are stacked before every \(\texttt{POOL}\) layer. This is generally a good idea for larger and deeper networks, because multiple stacked \(\texttt{CONV}\) layers can develop more complex features of the input volume before the destructive pooling operation.
LeNet-5 (LeCun et al, 1998)
Composition of two \(\texttt{CONV}+\texttt{POOL}\) layers, followed by a block of fully-connected layers.
Credits: Dive Into Deep Learning, 2020.
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 6, 28, 28] 156
ReLU-2 [-1, 6, 28, 28] 0
MaxPool2d-3 [-1, 6, 14, 14] 0
Conv2d-4 [-1, 16, 10, 10] 2,416
ReLU-5 [-1, 16, 10, 10] 0
MaxPool2d-6 [-1, 16, 5, 5] 0
Conv2d-7 [-1, 120, 1, 1] 48,120
ReLU-8 [-1, 120, 1, 1] 0
Linear-9 [-1, 84] 10,164
ReLU-10 [-1, 84] 0
Linear-11 [-1, 10] 850
LogSoftmax-12 [-1, 10] 0
================================================================
Total params: 61,706
Trainable params: 61,706
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.00
Forward/backward pass size (MB): 0.11
Params size (MB): 0.24
Estimated Total Size (MB): 0.35
----------------------------------------------------------------AlexNet (Krizhevsky et al, 2012)
Composition of a 8-layer convolutional neural network with a 3-layer MLP.
The original implementation was made of two parts such that it could fit within two GPUs.
LeNet vs. AlexNet
Credits: Dive Into Deep Learning, 2020.
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 64, 55, 55] 23,296
ReLU-2 [-1, 64, 55, 55] 0
MaxPool2d-3 [-1, 64, 27, 27] 0
Conv2d-4 [-1, 192, 27, 27] 307,392
ReLU-5 [-1, 192, 27, 27] 0
MaxPool2d-6 [-1, 192, 13, 13] 0
Conv2d-7 [-1, 384, 13, 13] 663,936
ReLU-8 [-1, 384, 13, 13] 0
Conv2d-9 [-1, 256, 13, 13] 884,992
ReLU-10 [-1, 256, 13, 13] 0
Conv2d-11 [-1, 256, 13, 13] 590,080
ReLU-12 [-1, 256, 13, 13] 0
MaxPool2d-13 [-1, 256, 6, 6] 0
Dropout-14 [-1, 9216] 0
Linear-15 [-1, 4096] 37,752,832
ReLU-16 [-1, 4096] 0
Dropout-17 [-1, 4096] 0
Linear-18 [-1, 4096] 16,781,312
ReLU-19 [-1, 4096] 0
Linear-20 [-1, 1000] 4,097,000
================================================================
Total params: 61,100,840
Trainable params: 61,100,840
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.57
Forward/backward pass size (MB): 8.31
Params size (MB): 233.08
Estimated Total Size (MB): 241.96
----------------------------------------------------------------VGG (Simonyan and Zisserman, 2014)
Composition of 5 VGG blocks consisting of \(\texttt{CONV}+\texttt{POOL}\) layers, followed by a block of fully connected layers. The network depth increased up to 19 layers, while the kernel sizes reduced to 3.
AlexNet vs. VGG
Credits: Dive Into Deep Learning, 2020.
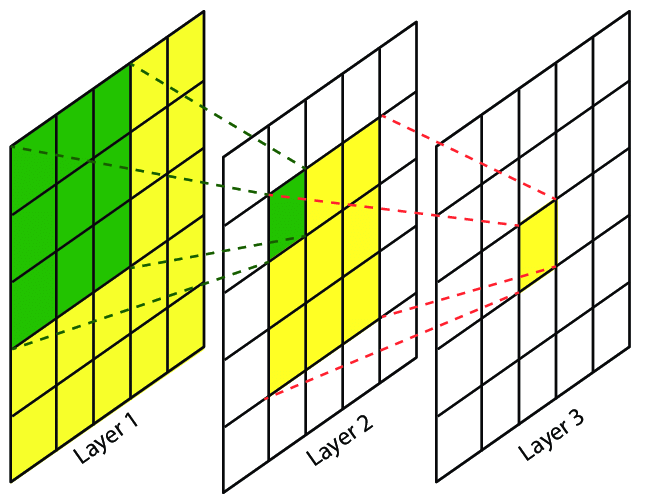
The effective receptive field is the part of the visual input that affects a given unit indirectly through previous convolutional layers. It grows linearly with depth.
E.g., a stack of two \(3 \times 3\) kernels of stride \(1\) has the same effective receptive field as a single \(5 \times 5\) kernel, but fewer parameters.
----------------------------------------------------------------
Layer (type) Output Shape Param #
================================================================
Conv2d-1 [-1, 64, 224, 224] 1,792
ReLU-2 [-1, 64, 224, 224] 0
Conv2d-3 [-1, 64, 224, 224] 36,928
ReLU-4 [-1, 64, 224, 224] 0
MaxPool2d-5 [-1, 64, 112, 112] 0
Conv2d-6 [-1, 128, 112, 112] 73,856
ReLU-7 [-1, 128, 112, 112] 0
Conv2d-8 [-1, 128, 112, 112] 147,584
ReLU-9 [-1, 128, 112, 112] 0
MaxPool2d-10 [-1, 128, 56, 56] 0
Conv2d-11 [-1, 256, 56, 56] 295,168
ReLU-12 [-1, 256, 56, 56] 0
Conv2d-13 [-1, 256, 56, 56] 590,080
ReLU-14 [-1, 256, 56, 56] 0
Conv2d-15 [-1, 256, 56, 56] 590,080
ReLU-16 [-1, 256, 56, 56] 0
MaxPool2d-17 [-1, 256, 28, 28] 0
Conv2d-18 [-1, 512, 28, 28] 1,180,160
ReLU-19 [-1, 512, 28, 28] 0
Conv2d-20 [-1, 512, 28, 28] 2,359,808
ReLU-21 [-1, 512, 28, 28] 0
Conv2d-22 [-1, 512, 28, 28] 2,359,808
ReLU-23 [-1, 512, 28, 28] 0
MaxPool2d-24 [-1, 512, 14, 14] 0
Conv2d-25 [-1, 512, 14, 14] 2,359,808
ReLU-26 [-1, 512, 14, 14] 0
Conv2d-27 [-1, 512, 14, 14] 2,359,808
ReLU-28 [-1, 512, 14, 14] 0
Conv2d-29 [-1, 512, 14, 14] 2,359,808
ReLU-30 [-1, 512, 14, 14] 0
MaxPool2d-31 [-1, 512, 7, 7] 0
Linear-32 [-1, 4096] 102,764,544
ReLU-33 [-1, 4096] 0
Dropout-34 [-1, 4096] 0
Linear-35 [-1, 4096] 16,781,312
ReLU-36 [-1, 4096] 0
Dropout-37 [-1, 4096] 0
Linear-38 [-1, 1000] 4,097,000
================================================================
Total params: 138,357,544
Trainable params: 138,357,544
Non-trainable params: 0
----------------------------------------------------------------
Input size (MB): 0.57
Forward/backward pass size (MB): 218.59
Params size (MB): 527.79
Estimated Total Size (MB): 746.96
----------------------------------------------------------------ResNet (He et al, 2015)
Composition of first layers similar to GoogLeNet, a stack of 4 residual blocks, and a global average pooling layer. Extensions consider more residual blocks, up to a total of 152 layers (ResNet-152).
Regular ResNet block vs. ResNet block with \(1\times 1\) convolution.
.footnote[Credits: Dive Into Deep Learning, 2020.]
Training networks of this depth is made possible because of the skip connections in the residual blocks. They allow the gradients to shortcut the layers and pass through without vanishing.
Credits: Dive Into Deep Learning, 2020.
The benefits of depth
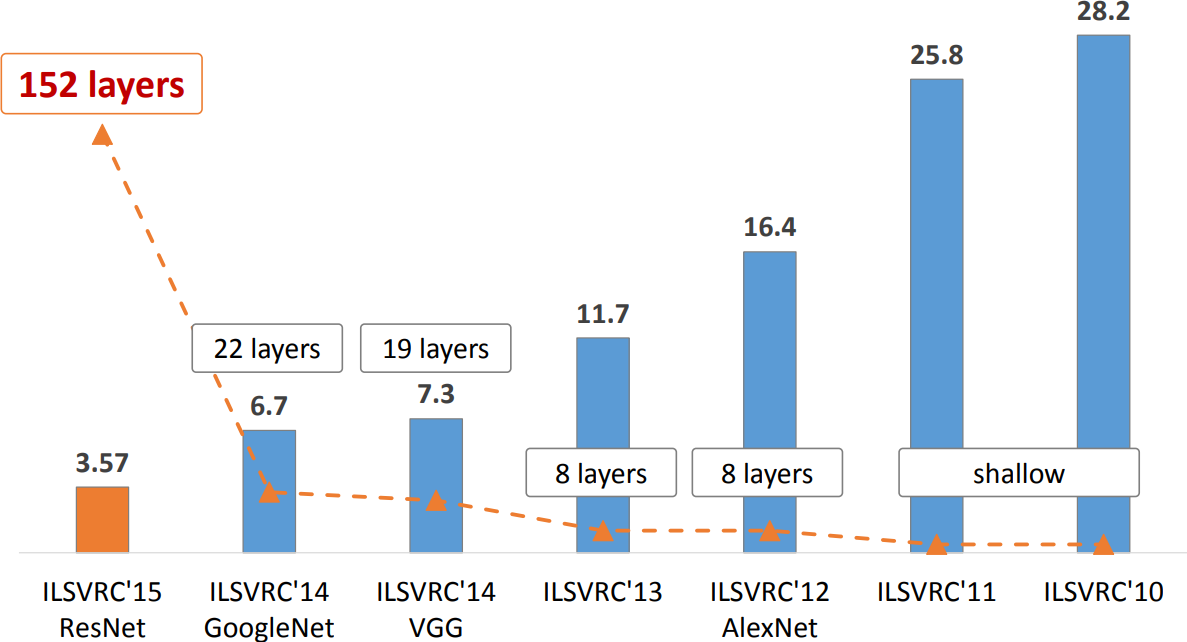
Under the hood
Understanding what is happening in deep neural networks after training is complex and the tools we have are limited.
In the case of convolutional neural networks, we can look at:
- the network’s kernels as images
- internal activations on a single sample as images
- distributions of activations on a population of samples
- derivatives of the response with respect to the input
- maximum-response synthetic samples
Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
Looking at filters
LeNet’s first convolutional layer, all filters.
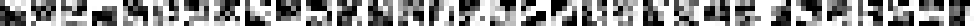
Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
LeNet’s second convolutional layer, first 32 filters.
.
Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
AlexNet’s first convolutional layer, first 20 filters.

Credits: Francois Fleuret, EE559 Deep Learning, EPFL.
Maximum response samples
Convolutional networks can be inspected by looking for synthetic input images \(\mathbf{x}\) that maximize the activation \(\mathbf{h}_{\ell,d}(\mathbf{x})\) of a chosen convolutional kernel \(\mathbf{u}\) at layer \(\ell\) and index \(d\) in the layer filter bank.
These samples can be found by gradient ascent on the input space: \[\begin{aligned} \mathcal{L}_{\ell,d}(\mathbf{x}) &= ||\mathbf{h}_{\ell,d}(\mathbf{x})||_2\\ \mathbf{x}_0 &\sim U[0,1]^{C \times H \times W } \\ \mathbf{x}_{t+1} &= \mathbf{x}_t + \gamma \nabla_{\mathbf{x}} \mathcal{L}_{\ell,d}(\mathbf{x}_t) \end{aligned}\]

VGG-16, convolutional layer 1-1, a few of the 64 filters
Credits: Francois Chollet, How convolutional neural networks see the world, 2016.

VGG-16, convolutional layer 2-1, a few of the 128 filters
Credits: Francois Chollet, How convolutional neural networks see the world, 2016.

VGG-16, convolutional layer 3-1, a few of the 256 filters
Credits: Francois Chollet, How convolutional neural networks see the world, 2016.

VGG-16, convolutional layer 4-1, a few of the 512 filters
Credits: Francois Chollet, How convolutional neural networks see the world, 2016.

VGG-16, convolutional layer 5-1, a few of the 512 filters
Credits: Francois Chollet, How convolutional neural networks see the world, 2016.
Some observations:
- The first layers appear to encode direction and color.
- The direction and color filters get combined into grid and spot textures.
- These textures gradually get combined into increasingly complex patterns.
The network appears to learn a hierarchical composition of patterns.

What if we build images that maximize the activation of a chosen class output?
The left image is predicted with 99.9% confidence as a magpie!


Credits: Francois Chollet, How convolutional neural networks see the world, 2016.
Deep Dream. Start from an image \(\mathbf{x}_t\), offset by a random jitter, enhance some layer activation at multiple scales, zoom in, repeat on the produced image \(\mathbf{x}_{t+1}\).
Biological plausibility
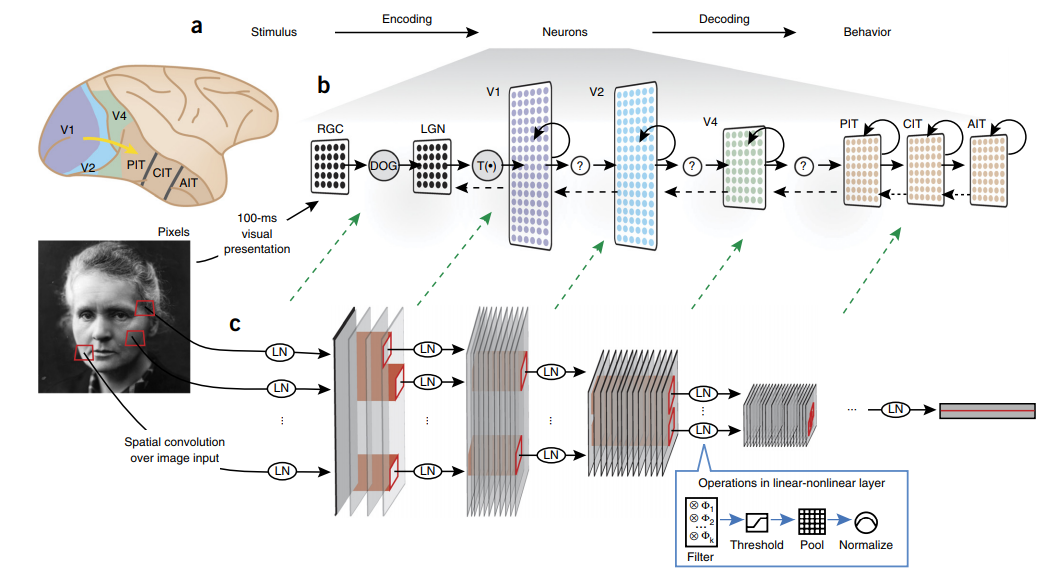
“Deep hierarchical neural networks are beginning to transform neuroscientists’ ability to produce quantitatively accurate computational models of the sensory systems, especially in higher cortical areas where neural response properties had previously been enigmatic.”
Credits: Yamins et al, Using goal-driven deep learning models to understand sensory cortex, 2016.
Exercises
Further reading
(optional)
- Francois Fleuret, Deep Learning Course, 4.4. Convolutions, EPFL, 2018.
- Yannis Avrithis, Deep Learning for Vision, Lecture 1: Introduction, University of Rennes 1, 2018.
- Yannis Avrithis, Deep Learning for Vision, Lecture 7: Convolution and network architectures, University of Rennes 1, 2018.
- Olivier Grisel and Charles Ollion, Deep Learning, Lecture 4: Convolutional Neural Networks for Image Classification, Université Paris-Saclay, 2018.
- Rosenblatt, F. (1958). The perceptron: a probabilistic model for information storage and organization in the brain. Psychological review, 65(6), 386.
- Bottou, L., & Bousquet, O. (2008). The tradeoffs of large scale learning. In Advances in neural information processing systems (pp. 161-168).
- Rumelhart, D. E., Hinton, G. E., & Williams, R. J. (1986). Learning representations by back-propagating errors. nature, 323(6088), 533.